u 教材类别:图形推理
u 实施对象:高中以上,欲参加国家考试者
背景:
图形推理是国内公务员考试中,判断推理每年的必考题型,题量为5—10道不等。图形推理展现了文化公平的特点,指测验内容对不同知识背景(包括所学专业、学历水平、文化背景、工作背景等方面)的人员是适当而且公平的。
主要考查考生的观察、抽象和推理的能力。
图形推理大致可以分为两大类:
一类是规律类,主要包含样式类、位置类、数量类。
另一类是重构类,主要包含平面重构和空间重构。
教学设计:
以3人为单位分作小组。
在过程中,小组间可藉由思考及彼此讨论,试著找到最适合答案及解释。
1. 依照题目分类,给予受试者范例、例题
2. 给予大范围提示,如图形元素,或是数量关係等
3. 给予正确答案,并让受试者思考为何
4. 给予解析,并让受试者重新思考验证
5. 使受试者熟悉题目类型,学习找到关键点、反覆推演
以下为测验题目之解析:
【例1】

【答案】B
【解析】相互分离的首先数元素数量,每个图形都有3个元素组成,答案为B。
【例2】
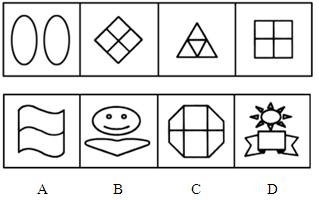
【答案】A
【解析】每个图形都只有一种元素,答案为A。
【例3】

【答案】D
【解析】本题虽然也是考查元素,但是会发现无论是从元素数量入手还是从元素的种类入手都无法攻克这个题目。观察整个图形会发现,一共只有两种元素,一个圆圈一个方,而没幅图中圆的个数减去方的个数等于2,答案为D。
【例4】
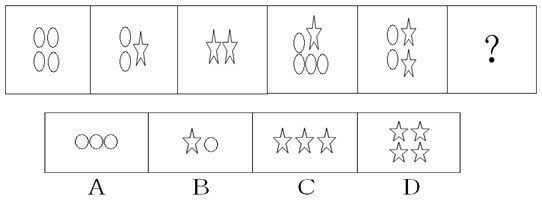
【答案】C
【解析】考查两种元素之间的换算。一个星星=三个圆圈,换算之后构成45678?的等差数列,答案为C。
归纳整理-依元素类为例
观察后可以快速的发现元素数量和元素种类这两点,但归纳统整后其实元素类的题目一共有四种解法的。
(1)元素数量,即相互独立的部分。
(2)元素的种类。
(3)两种元素之间的运算,通常有加减乘除运算。
(4)两种元素之间的换算。换算完之后一般情况下呈等差数列或等比数列。
验证教学成效
实验分组
u 实验组:经分组讨论及解析教学之受试者
u 对照组:未经分组讨论及解析教学之受试者
以个人为单位进行测验,受试者彼此不能进行任何讨论
预期成效:
有经过分组讨论及解析教学之受测者(实验组),测验成果将比未经分组讨论及解析教学(对照祖)来得更好。

